تعلّم البرمجة بلغة كوتلن (46): دوال اللامبدا Lambdas


|
استمع إلى المقال
|
تعرّفنا في درس الدوال، كيفية الإعلان عنها واستدعائها، وما الذي يمكنها القيام به. في هذا القسم بداية من هذا الدرس، سنتعرّف على طريقة مختلفة لاستخدام الدوال في شفرتنا. بدراسة تطبيقات لغة كوتلن، لميزات البرمجة الوظيفية (الدّالية)، مثل التعامل مع الدوال تمامًا كما لو كائنات. أو إرسال دالة، إلى دالة اخرى كمعامل Parameter، أو كتابة دالة مجهولة بدون إسم، أو أن تستدعي الدالة نفسها بطريقة تكرارية مستمرة.
وغيرها من الميزات التي تجعل من شفرة برنامجنا، أكثر نظافةً وترتيبًا وقابلية للقراءة والصيانة، كما سنرى في سلسلة الدروس التالية.
البساطة هي الثمن الذي لا مفر من دفعه للحصول على الموثوقية.
توني هور – عالم حاسوب
عند البدء في تعلم البرمجة، نبدأ غالبًا باستخدام نمط البرمجة الأمرية Imperative programming. والذي يكون بإعطاء الحاسب، مجموعة من التعليمات أو الأوامر، واحدة تلو الأخرى. وهو نفس النمط الذي استخدمناه كثيرًا في هذه الدورة حتى الآن.
ولفهم هذا النمط، يمكننا النظر إلى الشفرة التالية:
لدينا قائمة List من الأعداد الصحيحة (فردية وزوجية) أسندناها للمتغير numbers. ما نريد فعله، هو فلترة filter القائمة numbers، والبحث عن الأعداد الزوجية فقط، ثم إضافتها لقائمة أخرى. لذلك، أنشأنا قائمة ثانية أسميناها evenNumList من نوع القوائم التي تقبل التغيير MutableList حتى نستطيع إضافة الأعداد الزوجية لها.
للبحث عن الأعداد الزوجية بين عناصر القائمة numbers، لابد من أن ندور عليها عنصرًا بعد عنصر، باستخدام حلقة التكرار for. داخل for، لدينا كتلة if والتي وضعنا بها شرط: إذا كان أي عنصر في القائمة numbers عند قسمته على 2 يتبقى صفر، نضيفه إلى القائمة evenNumList باستخدام دالة ()add.
وأخيرًا، بعد أن تنتهي حلقة الـ for ويتم إضافة الأعداد لقائمة evenNumList، نطبع القائمة الجديدة عبر دالة ()println والتي ستظهر كالتالي:
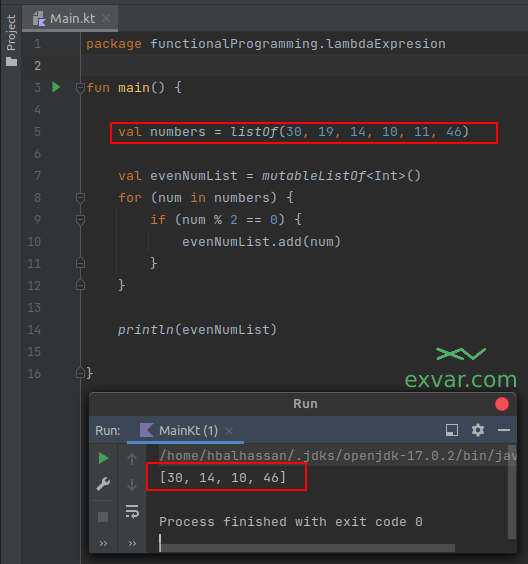
كما نرى في الشفرة أعلاه، يتميز هذا النمط البرمجي ببساطته، لتوجيهه أوامر مباشرة لمترجم اللغة، والذي سينفذها سطرًا تلو الآخر. وبساطته هذه، هي ما تجعله سهل الفهم والتطبيق، لذا من الطبيعي أن نبدأ به تعلم البرمجة.
ولكن، عند استخدامه في كتابة البرامج كبيرة الحجم، ستؤدي هذه البساطة الظاهرة إلى عكس ذلك تمامًا. ستصبح الشفرات المتراكمة، معقدة وصعبة الفهم. بالتالي سيكون برنامجنا مليء بالأخطاء، وغير قابل للصيانة، وصعب الإختبار.
نمط البرمجة الوظيفية هو أحد البدائل المناسبة لمعالجة المشاكل الناتجة عن البرمجة الأمرية.
هو نمط تكون فيه الدوال، هي الأساس في كتابة شفرات البرامج. وهو يعمل بالطريقة التالية:
خذ المدخلات Inputs في البرنامج، وطبّق عليها سلسلة من الوظائف عبر استخدام الدوال Functions، للحصول على المخرجات Outputs أو النتائج.
قد يبدو هذا الأمر بسيطًا، ولكن لإستخدام هذا النمط، هناك الكثير من القواعد التي يجب إتباعها. مثل الطريقة المثلى لإنشاء الدوال، وما هو النطاق الذي يمكن أن يتأثر بالتغييرات التي تحدثها هذه الدوال.
دوال اللامبدا هي إحدى تطبيقات كوتلن للبرمجة الوظيفية. وإن لم تكن كوتلن هي أول من استخدمتها، فقد كانت موجودة في لغات أخرى لسنوات قبلها. ولكن على كل حال، تُستخدم دوال اللامبدا في مشاريع كوتلن بصورة مكثفة. لذا من الصعب جدًا فهم هذه المشاريع أو لغة كوتلن نفسها، دون الفهم الصحيح لهذه الدوال وكيفية عملها.
وقبل أن نعرف المزيد عن كتابة اللامبدا واستخداماتها، دعونا نتعرّف أولًا على نوع بيانات الدوال في كوتلن.
نحن نعرف أن للكائنات أنواع بيانات متعددة. فمثلاً، النص التالي هو كائن من النوع String:
val language: String = "Kotlin"وبما أن المتغير language هو المرجع الذي نستخدمه للوصول لقيمة الكائن النصي من النوع String والذي قيمته هي الكلمة “Kotlin”، فسيكون نوع بيانات هذا المتغير هو String. وهو ما كتبناه صراحة بعد اسم المتغير والنقطتين المتعامدتين (:).
ولكن لأن كوتلن لديها نظام استنتاج الأنواع Type inference، يمكننا التخلي عن كتابة النوع بعد اسم المتغير صراحة:
val language = "Kotlin"هذا الأمر ينطبق على كل أنواع البيانات في كوتلن، أو حتى الكائنات من الأصناف الخاصة بنا، كما شرحناه تفصيلياً في دروس قسم مقدمة في الكائنات.
تماماً مثل الكائنات، لدى كوتلن دعم مدمج يأتي افتراضيًا مع اللغة لأنواع بيانات الدوال. ويتم التعامل معه، بنفس الطريقة التي يتم التعامل بها مع أنواع بيانات الكائنات.
فإذا كانت الدالة لديها معاملات وتعيد قيمة من نوع بيانات معين، فسيكون نوع بياناتها هو:
(parameters types) -> return value typeنضع المعاملات بين قوسين مع الفصل بينها بفاصلة ( , ) ثم سهم <- ثم نوع البيانات الذي تعيده الدالة. أما إذا لم يكن لدى الدالة معاملات ولا تعيد قيمة، فسيكون شكل نوع بياناتها كالتالي:
() -> Unitكما نرى القوسين في نوع بيانات الدالة فارغين، للدلالة على أن الدالة ليس لديها معاملات. ثم بعد السهم يأتي النوع Unit، وهو النوع الافتراضي للدوال التي لا تعيد قيمة من نوع بيانات معيّن.
كمثال، إذا كان لدينا دالة بسيطة لجمع عددين، وأسميناها sum:
fun sum(a: Int, b: Int) : Int {
return a + b
}نوع بيانات دالة ()sum، هو:
(Int, Int) -> Intوهذا يعني أن دالة ()sum، تأخذ معاملين parameters من النوع Int، وتكون نتيجة التعبير العائد منها، هي أيضًا من النوع Int.
أمّا إذا كانت لدينا دالة بدون معاملات، ولا تعيد نتيجة من نوع بيانات معين مثل:
fun sayHello() {
println(“Hello World”)
}نوع بيانات دالة ()sayHello، هو:
() -> Unitلأنها دالة بدون معاملات، لذا قوسي نوع بياناتها، فارغين. ولأنها تقوم بإجراء معين لا يعيد أية نتيجة، فهذا يعني في كوتلن أنها تعيد النوع Unit.
وهكذا يكون لكل دالة، نوع بيانات معين، حسب معاملاتها، وحسب نوع النتيجة التي تعيدها.
يمكن كتابة اللامبدا بدون اسم، وبدون الكلمة المفتاحية للدوال fun. وتكون في أبسط صورها:
val lambdaName: () -> Unit = { println("Hello World") }حيث lambdaName هو المتغير الذي سيتم إسناد تعبير اللامبدا إليه. ونوع بياناته هو Unit <- ()، وهو نوع بيانات دالة اللامبدا. أمّا الشفرة ما بين الأقواس المعقوفة { }، هي التي تسمى تعبير لامبدا.
يمكننا كتابة لامبدا أكثر تعقيدًا، كأن تكون دالة تستقبل معاملات، وتعيد نتيجة من نوع بيانات معين، مثل:
val square: (Int) -> Int = { n1: Int -> n1 * n1}تعبير اللامبدا هذا، لديه معامل واحد من النوع Int ويجري عملية ضرب المعامل على نفسه ويعيد نتيجة من النوع Int أيضًا. لذلك عند إسناده إلى المتغير square، سيكون نوع بيانات المتغير هو:
(Int) -> Intأي أن هذا المتغير يستقبل قيمة من النوع Int، ثم عبر اللامبدا يجري عملية الضرب، ويعيد نتيجة من النوع أعلاه.
نلاحظ أيضًا أنه داخل الأقواس المعقوفة للامبدا، كتبنا التالي:
n1: Int ->هذا هو معامل اللامبدا أسميناه n1 ونوع بياناته Int. ويأتي بعده سهم <- يفصله عن الجسم الفعلي للامبدا وهي الشفرة التي تقوم بالإجراء.
الآن يمكننا استخدام هذا المتغير كالتالي:
println(square(3))وسيتم طباعة الرقم 9، وهو مربع الرقم 3 المرسل للامبدا عبر المتغير الذي يُمثلها square.
قلنا في الفقرة أعلاه، أن الشفرة بين الأقواس المعقوفة هي دالة اللامبدا:
{ n1: Int -> n1 * n1}وهي دالة لامبدا تستقبل قيمة من النوع Int عبر المعامل n1. ثم بعد السهم، تقوم بالإجراء المطلوب، وهو في شفرتنا أعلاه ضرب المعامل في نفسه.
ولكن كما نرى، أن دالة اللامبدا بدون اسم، إذا كيف يمكننا استدعائها؟ حسنًا، لنتمكن من استخدام دالة اللامبدا هذه، إحدى الطرق هي أن نسندها لمتغير، كما فعلنا في الفقرة السابقة مع المتغير square. أمّا الطريقة الثانية، هي أن نرسلها كقيمة Argument لمعامل Parameter يخصُّ دالة أخرى، إذا كانت الدالة الأخرى لديها معامل من نوع بيانات الدوال.
لفهم الطريقة الثانية، سنستخدمها في تحسين شفرتنا التي كتبناها في بداية هذا الدرس.
تنتشر دوال اللامبدا بصورة مكثفة في مكتبة كوتلن القياسية. لذا لتحسين شفرتنا من بداية هذا الدرس، يمكننا إعادة كتابتها باستخدام هذه الدوال، مثل دالة ()filter:
للحصول على الأعداد الزوجية من القائمة numbers، استخدمنا هذه المرة دالة ()filter، والتي تستقبل تعبير Lambda. نلاحظ أنه داخل الأقواس المعقوفة لدالة اللامبدا، وضعنا المتغير num وهو من النوع Int، لأنه يُمثِّل عنصر واحد من قائمة numbers المُراد البحث فيها. ثم حددنا قاعدة البحث لدالة ()filter، بـ:
num % 2 == 0بهذه الطريقة، كأننا نقول لدالة ()filter، البحث عن كل عنصر num من القائمة numbers، يكون باقي قسمته على 2، يساوي صفر. باستخدام هذه المعادلة، ستكون نتيجة عمل دالة ()filter، هي قائمة List جديدة تحتوي على الأعداد الزوجية فقط، وهي القائمة التي سيتم إسنادها إلى المتغير evenNumList.
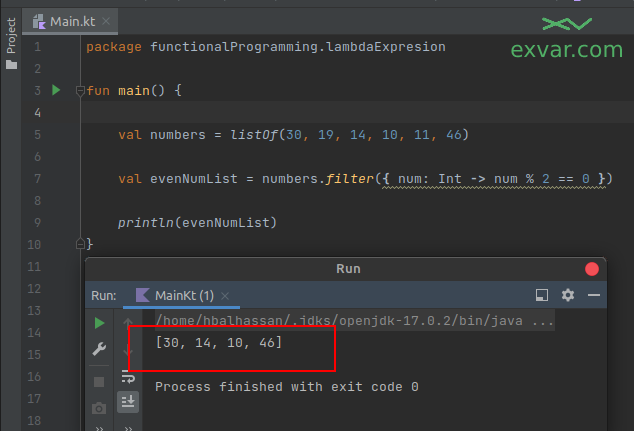
هذه المرة أيضًا، ستكون نتيجة الطباعة هي نفس النتيجة عند استخدام التعليمات الأمرية المباشرة التي رأيناها في بداية هذا الدرس، وهي طباعة الأعداد الزوجية وتجاهل الفردية:
عند إسناد دالة اللامبدا إلى متغير، يمكننا حذف نوع بيانات الدالة الذي يأتي بعد اسم المتغير. لأن مترجم كوتلن، سيتعرف على نوعه من اللامبدا نفسها:
val square = { n1: Int -> n1 * n1}أمّا عند إرسال دالة اللامبدا إلى دالة أخرى مثل دالة ()filter، فيمكن استبدال المعامل بالكلمة it، إذا كان لدى اللامبدا معامل واحد فقط.
فمثلًا، عند استخدام ()filter مع القائمة numbers، كتبنا المعامل num ونوع بياناته صراحةً، للتعبير عن كل عنصر في القائمة. ولأنه معامل واحد فقط، لا داعي لتكراره واستبداله بالكلمة it، وسيفهم مترجم كوتلن المقصود:
val evenNumList = numbers.filter({ it % 2 == 0 })تحسين آخر يمكننا استخدامه، وهو حذف أقواس الدالة التي تستقبل تعبير اللامبدا، إذا كان لديها معامل من النوع دالة واحد فقط، أو إذا كان هو المعامل الأخير فيها. ولأن هذا هو حال دالة ()filter، يمكننا حذف أقواسها واستدعائها كالتالي:
val evenNumList = numbers.filter { it % 2 == 0 }وعند تنفيذ هذه الشفرة بعد التحسين، ستكون نتيجة التنفيذ هي نفسها كالسابق.
كما نرى، أن نمط البرمجة الوظيفية أكثر سهولة في الكتابة وأكثر ترتيبًا وفهمًا. فبمجرد رؤية دالة ()filter، سنعرف ما الذي تقوم به هذه الشفرة. خلافًا للنمط الأمري، والذي علينا تتبع الشفرة وقراءة ما يحدث في حلقة التكرار وغيرها. ويكون هذا الأمر أصعب، إذا كانت الشفرة كبيرة جدًا.
إذا أردنا أيضًا طباعة الأعداد الفردية من القائمة numbers، يمكن باستخدام نمط التعليمات المباشرة، إنشاء قائمة أخرى نحفظ بها الأعداد الفردية وطباعتها منفصلة.
أو يمكننا بكل بساطة، استخدام دالة لامبدا أخرى من مكتبة كوتلن القياسية مثل دالة ()partition:
تمامًا مثل دالة ()filter نرسل لدالة ()partition الأساس أو القاعدة التي ستستخدمها للقيام بإجراء على القائمة التي تستدعيها. ما ستقوم به هذه الدالة، هو تقسيم قائمة numbers إلى قائمتين. القائمة الأولى، سيكون بها العناصر التي توافق الشرط المرسل لها عبر اللامبدا. أمّا القائمة الثانية، فتشمل العناصر التي لا توافق الشرط.
ولأن الدالة ستعيد كائن Pair يحتوي على قائمتين من النوع List، تمكنّا من استخدام ميزة تفكيك التصريحات، وفككنا الكائن Pair إلى متغيرين (evenList, oddList).
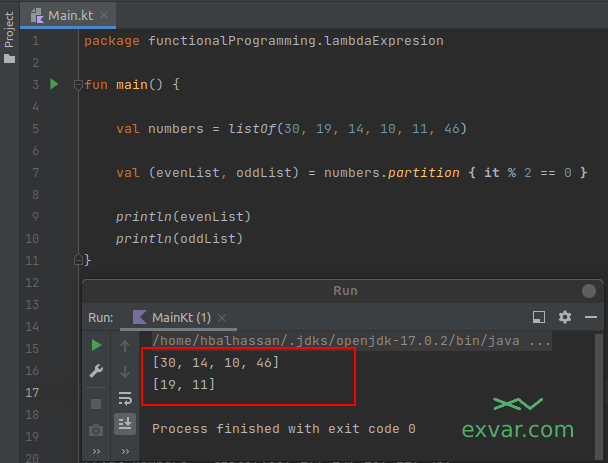
وعند تنفيذ الشفرة أعلاه، ستكون نتيجة الطباعة هي:
يمكننا استخدام دالة ()map، لتحويل Transformation عناصر التجميعات مثل تجميعة القوائم Lists، كما نريد. تعيد دالة ()map قائمة أخرى، بعد تطبيق الشرط المُرسل لها عبر اللامبدا:
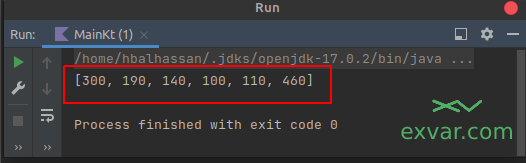
في الشفرة أعلاه، نطلب من دالة ()map، تحويل عناصر قائمة numbers إلى عناصر مختلفة، بضرب كل منها بالرقم 10. وبعد أن تقوم الدالة بتحويل العنصر، ستضيفه إلى قائمة جديدة. وفي النهاية ستعيد الدالة هذه القائمة، ليتم حفظها في المتغير newNumbers. بعد تنفيذ الشفرة، ستكون نتيجة طباعة القائمة الجديدة:
تعرّفنا في هذا الدرس، على ما هي اللامبدا وكيف يمكننا كتابتها واستخدامها مع الدوال من مكتبة كوتلن القياسية. في الدروس القادمة في هذا القسم، سنتعلم المزيد عن اللامبدا وتطبيقات البرمجة الوظيفية في كوتلن عمومًا.
هذا الدرس هو جزء من سلسلة تعليم مبادئ البرمجة بلغة كوتلن. لمُتابعة الدروس منذ البداية ومُشاهدة فهرس المحتويات يمكنك الانتقال إلى الدرس الأول من هنا.
هل أعجبك المحتوى وتريد المزيد منه يصل إلى صندوق بريدك الإلكتروني بشكلٍ دوري؟
انضم إلى قائمة من يقدّرون محتوى إكسڤار واشترك بنشرتنا البريدية.



